Chaos and Complexity
There is a reasonable consensus on what the study of chaotic systems means, but there is very little consensus on what the study of complexity entails – it is a vaguely defined emerging field that is currently an unwieldy alliance of problems, aspirations, insights, and technologies. Most definitions start with a minimum requirement that many parts are involved in nonlinear interactions which create a whole with emergent properties. These properties are 'emergent' because they cannot be predicted from what is known about the parts and their relationships. Thus far, such systems can be modeled on computers, so that we can find out what actually does emerge from a known set of interactions, even if we cannot predict it. As soon as we introduce the idea that the parts should have agency, we enter a whole new minefield, because we cannot even know what are the relevant properties of the parts.
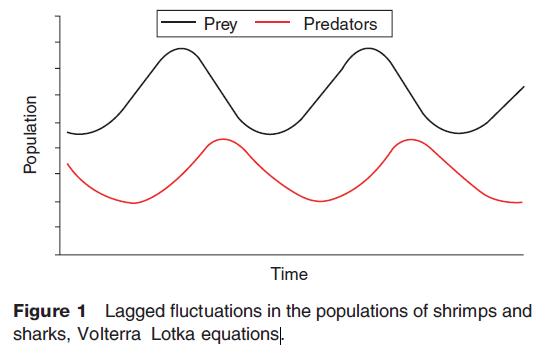
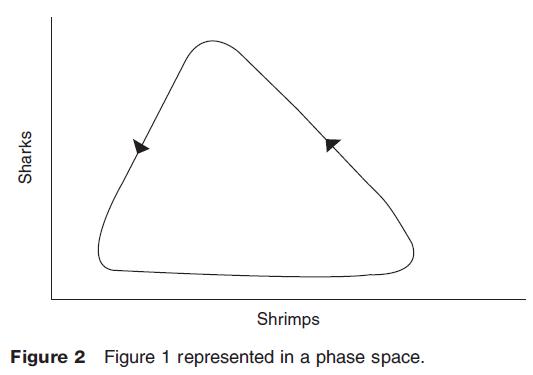
Without computers, systems theorists were able to make only small advances in understanding fluctuating system behavior. Volterra derived equations for the interaction of two species in an ecosystem, using nonlinear functions. The classic example is the relationship between basking sharks and shrimps. If the abundance of shrimps is low, the sharks starve, and there is a population crash. The shrimps can undergo a population explosion, since sharks reproduce slowly. But when the sharks do increase, shrimps decrease at an accelerating rate. The relationships are nonlinear, that is, the rate of change of one variable with respect to the other is not constant. The system results in 'repeated' fluctuations in the two species in time (Figure 1), which is indicated by the closed loop which shows the system in phase space (Figure 2). This behavior is often called dynamic equilibrium.
When small computers became available, systems theorists could run simulations of systems with more components. Although there had been mathematical intimations more than a century ago, it was not until these simulations were run that theorists finally understood there were classes of systems that never went to equilibrium, and never repeated a previous state. One of the first and a classic analysis of this was by the meteorologist Lorenz, who modeled the Earth's climate with three variables related to each other by nonlinear functions. Figure 3 shows how these three variables might change through time, and Figure 4 shows the behavior in phase space. Since the system revisits the same neighborhoods in space, we can say the path of the system has a kind of shape – here a shape with two lobes. This shape is known as a strange attractor. In this case, the system stays in one neighborhood for a while, then flips to the other ;neighborhood. The strange attractor actually exists in three dimensions, one for each variable. However, on two dimensional paper the diagram is also usually drawn in two dimensions, and it is important to realize the implications of this. These systems are deterministic – they have no random component. For any given current state, there is one and only one next state. This means that from any point in the phase space there can be one and only one line segment going to the next point. Hence, wherever in Figure 4 it appears that the lines touch and cross each other, they do not. They are separated in the third dimension, and pass either behind or in front of each other.
The trajectory of some systems can be modeled as a number, where each digit follows deterministically from the digit before. A system that goes to a stable end state might be something like this: 7826571974653843432222222222222. A system that reaches a dynamic equilibrium may be something like 78365913746525341414141414141. With chaotic behavior the number is essentially random, in that there is no detectable pattern in it, and it never goes to a terminal state. This understanding leads to the use of the apparently paradoxical term – deterministic randomness. It highlights the fact that the systems are deterministic, but that there is no way we can predict the value of the nth digit, without calculating all preceding n – 1 steps. The lack of predictability is a feature of randomness, but this kind of randomness does not come from flipping a coin. We will return to this feature in a discussion of measures of complexity, below.

So, we can summarize the main characteristics of chaotic behavior so far identified as: the system is deterministic, the system never repeats itself, and the system has a strange attractor. Now, consider the two lobes of Figure 4. Suppose one lobe represents ice age Earth, and the other, thermal period Earth. At some stage in the future, which state will the Earth be in? If the future we are thinking about is tomorrow (one iteration), then we have not much difficulty in saying tomorrow will be much like today. The only way we can find out what it will be like in 300 iterations, is to calculate all 300 steps. The future of the system is computationally irreducible. It is not that the system exhibits 'counterintuitive behavior'; the behavior has no intuitive characteristics. Further, if we change any of the initial conditions now by even the smallest amount, our prediction of tomorrow will change by an almost equally small amount, but the system in 300 iterations may be in a completely different state from the one calculated before. These systems are infinitely sensitive to initial conditions. This has been paraphrased as the 'butterfly effect': that a butterfly flapping its wings in West Africa may or may not set off dynamics that culminate in a hurricane in the Caribbean a month later. In history, the effect has been mythologized as: for want of a nail, a shoe was lost; for want of a shoe, a horse was lost; for want of a horse, a king was lost, and the kingdom too.
So, chaos theory is poorly named. It is not about randomness, it is about deterministic systems that are computationally irreducible. Further, it is about the im possibility of ever accurately mapping the real world onto such a system model. To do so, we would have to have an infinitely fine grained observation of the real world, and an infinitely large model. Increasing theoretical understanding of this problem has made us realize that we will never be able to predict the weather of northern temperate areas for more than a week, or two, at the most, by calculating forward from current system states. The present limitation of most weather forecasts to 5 days is because we are already nearing that limit. (This does not preclude some seasonal forecasting based on the historical understanding of repetitive behavior – as with El Nino or the North Atlantic Oscillation.)
Yet, although at first glance it might seem that we now 'know we cannot predict' the future, systems theorists have studied many different kinds of attractors, and to some extent can narrow down the range of possible futures.
Complexity
There may be a degree of agreement on the starting points for the study of complexity. But from then on, complexity becomes a circus big top for any number of performing intellectual animals, in an increasing number of circus rings.
The behavior of chaotic systems is a intuitive – that is, we cannot guess what they will do, we have to wait and see what they do. Complexity is one useful step beyond such a intuitive behavior. The dynamics of the system may well evoke in us some intuitive recognition of holistic behavior – as, for example, when a shoal of fish maintains a coherent pattern, but changes it to avoid a predator, or when a flock of birds seem to behave as a collective individual, forming and re forming a collective V shape as they fly on their migration routes. In these circumstances, we cannot predict exactly how the shoal or the flock will behave, but if we observe the same species, we begin to see the kinds of behavior that might occur. The same may be said of our understanding of riots in a football ground – we may know more about the pre conditions that might provoke or prevent a riot, but not be able to predict exactly when and in which part of the crowd it will start.
Increasing attention is now being paid to networks and emergent behavior. Networks may be richly connected, thinly connected, hierarchically connected, or of any combination. Increasingly we realize that the patterns of connectivity can have a significant effect on whether disruptions dissipate or propagate – as an example, it is clear that different patterns of road structure and connectivity affect the way jams develop and propagate, as any motorist on the UK's motorway network will know. Another example is a power grid in a large city, which collapses unpredictably when a minor fault trips a sequence of more significant faults. Put simply, we are only just beginning to develop the tools to understand how complex dynamics develop on different network structures.
The examples of fishes, birds, and humans were biological (in that nervous systems were involved): the example of the power system was physical. Some complexity theorists would claim that the two kinds of cases had the same basis, and that the distinction between biological and physical was 'old time disciplinarity' compared with the new interdisciplinarity. Others would claim that they are radically different, and cannot be fused. This dispute lies at the heart of our understanding of what is meant by 'science', and what is meant by 'being human'. In classical science the future is only an outcome of the present: the only questions that can be asked are 'how' questions, not 'why' questions. On the other hand, human beings believe they have agency, and can choose a future.
Both camps in complexity theory play with the idea of 'emergence'. This says that when some components are combined, there are properties of the whole that are not properties of the parts. At one level, this is trivially true (although still mysterious). Two gases, oxygen and hydrogen, combine together to make a compound, water, which has unique properties unlike those of either parent: its solid phase (ice) is less dense than its liquid phase, and hence ice floats. At other levels, it is nontrivially true. Time and again one can read in the literature that the most complex entity in the known universe is a human brain, and human beings have self consciousness. Where does this self consciousness come from? The only answer so far (if one accepts the question as meaningful) is that when a sufficient number of neurons are connected together (and it is a number in billions) consciousness 'emerges' as an effect which is not attributable to the properties of the neurons and synapses of the brain. That is to say, given enough quantity, quality changes.
Those who claim that the shoal of fish and the power system can belong to the same class of complexity are basing their claim on this idea that complexity emerges as a result of quantity – of elements, and of connections between elements. The problem is that with consciousness comes agency. For 'humanists' choosing a future implies that humans can imagine a model of a future, and that choice between them is purposive and not random. How do you explain behavior simultaneously as an 'outcome' and an 'intention'?
Cellular Automata
Cellular automata have been seized on by enthusiasts since computers have become ubiquitous to explore many aspects of what is claimed to be emergent behavior. In their simplest form, these are large 'boards' of many squares in a rectangular grid. The cells maybe either black or white. Any starting pattern of black and white may be used, and in any given simulation run, a set of transition rules is used to determine how a square may or may not change from black to white, or vice versa, in any one iteration.
If corner neighbors are counted, any square can have eight neighbors. For all unique combinations of black/white states for these nine cells, a transition rule specifies what the state of the central cell will be after the current iteration. There are therefore 29=512 black and white combinations of the nine squares overall that will give an output state of either black or white for the target square. For many starting states and for many transition rules, patterns simply go to some stagnant and possibly monotone state. However, there are examples where dynamic patterns emerge which seem to behave 'organically'. An exemplar of this is Conway's famous Game of Life. The reader is urged to visit the website for this game, to see many of the 'life forms' which emerge. The neurophilosopher Daniel Dennett used this game as a starting point for his attempt to show that there could be a solution to the 'outcome/intention' paradox in a book which has a similarly contradictory title: Freedom Evolves.
Just as systems that go to equilibrium or dynamic equilibrium are not of interest to the chaos theorist, so also the complexity theorist is not interested in those simulations which reach a static terminal state. By contrast, the others have many significant and interesting properties. They are computationally irreducible – only by running it 1000 iterations can you know what state it will be in after 1000 iterations. Each cell is a 'self ' with a boundary, and it has 'knowledge' of its own state and that of its immediate neighbors – so it is in an environment of which it has some knowledge, but not total knowledge. Its future states depend on how it reacts to its knowledge. Dynamic patterns self organize and higher scale (multicell) entities emerge, which have characteristic behavior patterns. Indeed this allure is so strong that there is an international club of people with their own vocabulary describing 'guns' and 'breeders' and 'gliders' that they have developed with their own sets of transition rules (Figure 5). 'Guns' are static shapes that fire 'projectiles' at regular intervals in straight directions; 'breeders' are shapes that produce new versions of themselves; 'gliders' are shapes that maintain their shape as they drift across the board.

Apparently this is a perfect metaphor for emergence, but actually it is not. The behavior of the whole is explicable by the behavior of the parts. Although it may appear that a 'breeder' is an organic whole, it has no self, no boundary to self, and no central knowledge processing. All of that still occurs at the level of the individual cells. The 'organisms' do not evolve – they might get eaten up or disintegrate, but the stable shapes that wander round the board do not randomly mutate and form new species. The simulations might however be good metaphors for the shoals of fish – there is no central processing there either, although an onlooker can sometimes get the sense that there could be. The behavior of the whole shoal may affect the survival of the species of fish, but this is an outcome, not an intention.
It is the human observer who imbues the fascinating patterns of Conway's 'game' with the dignity of 'life'. These 'creatures' lead frictionless lives in which they consume no negentropy, nor do they produce entropy. Notwithstanding this criticism, enthusiasts ardently pursue the field of artificial life (cyberlife), of which this simulation is a founding cornerstone.
Separately, there is no doubt considerable value in using these models to throw light on some kinds of complex dynamics. A favourite example is the modeling of traffic flows on motorways, where traffic can accelerate, then decelerate, and bunch up, often forming standing waves at points where there may have been an incident hours earlier. Running a model in which simple rules relate how cars adjust to each other in terms of spacing and speed can mimic these effects. In other complex networks like the power supply to the London Underground, if circumstances can be modeled which mimic a real world breakdown, then that does have a real world equivalent that we can construe as 'emergent', and one that we can usefully know more about.