Choice Modeling

Introduction

A conventional premise of microeconomic theory is that demand and supply are traded off through continuous adjustments in quantities. Individual demand is determined by calculus methods that maximize consumer utility (i.e., satisfaction), subject to constraints. By the 1970s, it had become clear from the pioneering work undertaken in transportation, marketing, and economics that many consumer decisions do not conform to this postulate of marginalist consumer theory. Individual decisions actually often involve a finite number of options that are indivisible, mutually exclusive, and collectively exhaustive. The determination of a 4 year college one is to attend upon high school graduation; the car make to buy; whether to buy a car, lease it, or neither; the commitment to marry; and the choice of a travel mode for one's daily commute are all examples of discrete choices that cannot be comprehended through the lens of conventional decision theory. Choice modeling is the theory of individual decisions among discrete alternatives and its empirical derivatives in the form of measurement pro cedures and estimation methods. Although choice models are commonly based on the postulate of rational behavior (a normative stance), they purport to be a faithful de scription of the expected behavior of individuals.

From rather narrow beginnings rooted in the econometrics of qualitative response variables and in the mathematical psychology of rational behaviors, choice modeling first addressed simple choice situations (for instance, 'where shall I do my grocery shopping this week?'), but quickly gained in robustness to cope with complex, multilevel systems of intertwined and constrained decisions. Choice models continue to contribute to the social science understanding of how human and social systems take shape from the coalescence of decisions of multiple actors (consumers and producers) based on utilitarian principles. They are also valued as operational models in various areas of applied spatial sciences, such as retail analysis, transportation, business site selection, housing, and real estate.

Human geographers mistakenly refer to spatial interaction models as choice models on occasions. If indeed equivalence has been established between certain forms of choice models, such as the multinomial logit model (MNL) presented hereunder, and entropy maximizing models of spatial interaction, the analogy is nevertheless in the algebraic form of the two models and not in the implied behaviors. Spatial interaction model ing is the subject of another article.

Theoretical Foundations

A simple choice problem can be conceptualized as the selection of one alternative from a predefined set of available discrete choice alternatives that are mutually exclusive and collectively exhaustive, which is also known as the choice set. In keeping with the view on consumer economics that utility cannot be derived from commodities per se, but from their objectively measurable characteristics, the utility of each alternative is evaluated on the basis of their intrinsic attributes as well as on the personal characteristics of the decision maker. The latter dependency accounts for interpersonal differences in the subjective perception and evaluation of alternative attributes. Following Thurstone's random utility theory, it is typically posited that, while individuals deterministically choose the alternative with the greatest utility, the utility of an alternative cannot possibly be known with full certainty. Unobserved preference factors and measurement errors and approximations account for the random component of utility. Hence, the model cannot forecast what choice is made, but it can estimate the likelihood that a given option in the choice set be selected.

The actual calculation of choice probabilities is contingent upon the specification of the error term (random utility) of the model. In early studies on discrete choice modeling, it was assumed for convenience sake that errors are independently and identically distributed as a double exponential function. Choice probabilities then take an elegant closed form known as the MNL. More formally, if n denotes an individual and i is an alternative, the probability that individual n chooses i has the form:

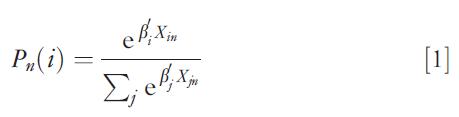
where b is a vector of parameters to estimate empirically and X is the vector of measurable characteristics of the alternatives that are variables in the systematic utility. For empirical reasons, the MNL is attractive and has become the workhorse of choice modeling due to its tractability and the relative ease with which its parameters can be estimated. Models based on other distributional assumptions of errors remain, to this day, less tractable. Assuming that errors are normally distributed, the socalled probit model has grown quite in popularity in recent years.

One of the noteworthy properties of the MNL that stems from the assumed distribution of errors is that it satisfies Luce's choice axiom and, therefore, exhibits independence from irrelevant alternatives (IIA). This entails that the ratio of choice probabilities of any two alternatives depends only on their systematic utility components and is totally unaffected by other alternatives that may be available to the decision maker. According to the choice axiom, no allowance whatsoever is made for different degrees of substitution or complementarity among choice alternatives. Consequently, any new alternative entering the choice set draws market share equally from each alternative already in the choice set. Whether the IIA property holds in the practice of specific decision situations has been the subject of considerable debate. If it does not hold, MNL predictions are biased and can be behaviorally counterintuitive. A famous illustration of this is Debreu's red bus/blue bus paradox whereby the introduction of a new bus service (red bus) competing against an existing bus service and private automobile would be forecasted by an MNL model to grant one third market share to each transport alternative, while intuition dictates that car would maintain a 50% market share and the balance would be split equally between the two bus services. This has led to alternative approaches to modeling discrete choices that impose less restriction on structures of substitution between alternatives.

Empirical Validation and Statistical Estimation

The implementation of discrete choice theory to real world decision situations involves significant measurement and statistical estimation issues. From the onset, two broad approaches have prevailed. In discrete choice models sensu stricto, actual choices are observed by survey and independent variables entering the utility function are either objective measures or subjective evaluations of the various choice alternatives of a prespecified choice set. The parameters of the utility function and the choice probabilities are estimated through data fitting procedures, usually a maximum likelihood method, so as to reveal preferences through calibration on overt behavior. This perspective has been very popular in transportation, housing, shopping, and other locational studies.

Alternatively, decompositional multiattribute preference models are estimated on the basis of an individual's stated preference ordering for a set of hypothetical choice alternatives. Choice set alternatives are composed according to principles of experimental design so as to insure statistical representativeness. Decompositional preference models first estimate the utility function of each individual on the separate contributions of each attribute level (using least squares regression analysis, analysis of variance, or linear programming), and apply a choice model to the resulting preference structure to simulate a choice outcome.

Each of the two approaches has different advantages and disadvantages. Because decompositional preference models are based on principles of experimental design, it is recognized that they can better account for the interpersonal heterogeneity in preferences. They can also handle choice alternatives that are beyond the realm of observation because they do not currently exist. This places them in a unique position to predict the success of new choice options, such as new forms of public transportation services, new electric automobile technologies, new supermarket concepts, or new concepts of housing developments, such as transit oriented developments and mixed use complexes as responses to the challenges of greater urban sustainability. It is undeniable, however, that the experimental nature of data collection in decompositional models renders them more complex, while the validity of their prediction of actual choices may be inferior to that of discrete choice models sensu stricto. Estimation procedures for combining revealed and stated preference data, along with psychometric data (i.e., attitudes and perceptions), have been available since the early 1990s and have been instrumental in enhancing the behavioral representation of the choice process.

Modeling Complex Choices

Admittedly, the choice model embodied by eqn [1] raises a number of issues regarding its behavioral underpinnings and its ability to capture more than just the simplest choice decisions made by human beings. These issues have driven the agenda of research on choice modeling for the past three decades.

Choice Set Formation and the Decision Process

The model of eqn [1] suggests that the choice set is known beforehand and independently of the choice process. In fact, the choice set of any single decision maker is a subset of the universe of all alternatives that are both feasible to the decision maker (living in the White House belongs to the realm of fiction for all practical purposes) and known at the time a decision is made (hence the power of advertising to raise people's awareness). Accordingly, individual behavior can be framed as a two step process wherein a choice set is specified first, and a selection among available alternatives is then made.

Using the universal choice set may be a poor surrogate for the decision maker's choice set because it fails to account for constraints precluding certain alternatives, such as their physical availability (e.g., absence of passenger train service between many US cities), time availability (e.g., a grocery store that is too remote for biweekly food purchases), affordability, and others. When a decision maker has no or limited knowledge of some perfectly feasible alternatives, these alternatives are in effect removed from one's choice set. Hence, proceeding with a model based on the universal choice set is bound to bias estimation results (a nonzero probability is falsely assigned to alternatives outside the choice set) and to impute to the nonselection of this alternative to individual preferences and free will instead of unawareness and infeasibility. Given these considerations and for pragmatic reasons of data availability and computational power, reduced choice sets are employed instead of universal choice sets in many decision situations of relevance to human geography. Ad hoc narrowing, sampling, and aggregation strategies are routinely implemented with reasonable success as far as the selection among geographically defined alternatives is concerned. Ad hoc narrowing of the choice set may be based on some distance cutoff or some other independent and well informed knowledge of behavioral decisions. By reducing the choice set to a manageable number of alternatives, these strategies are also instrumental in enabling the modeling of spatial choices, which routinely involve a very large number of possible alternatives (hundreds of restaurants in a mid to large size metropolitan area, tens of thousands of housing units for lease or for sale, etc.).

Having decision makers specify their own choice sets is a very controversial matter due to the inaccuracy of the information in the light of the fact that the choice set is not explicitly kept in memory by the decision maker. A somewhat less arbitrary and more systematic approach to the two stage choice problem process consists in the implicit approximation of the decision maker's choice set. This approximation proceeds by assigning a weight to each alternative to reflect its degree or likelihood of membership to the decision maker's choice set according to some preset rules such as geographic proximity or accessibility. Finally, the choice set can be explicitly de termined, in which case the choice process represented by eqn [1] is replaced by

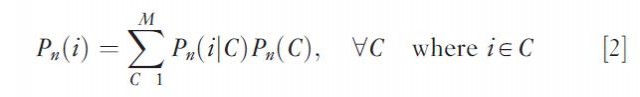
Here, the second term models a given choice set C from the universal choice set M as a function of personal and household characteristics of the decision maker (including one's locational profile) and of characteristics of the alternatives in choice set C; the first term involves the evaluation of alternative i conditional on choice set C. This framework has been successfully implemented in various spatial choice contexts, including the choice of shopping destinations.

Substitution among Alternatives

Because of its property of independence of irrelevant alternatives, the MNL (eqn [1]) imposes that all alternatives be uniformly substitutable (equal cross elasticities). The red bus/blue bus paradox illustrates the senselessness of this assumption in many decision situations. This is proven to be particularly the case with spatial decision making because choice alternatives exhibit well defined spatial structures resulting from adjustments to the preference of decision makers for minimizing effort in travel and search activities and from adjustments to the decision maker's processing of information on spatial alternatives into clusters based on geography. In other words, choice alternatives that are located nearby are closer substitutes than distant alternatives. A variety of choice modeling approaches exists that afford a richer pattern of substitution among alternatives.

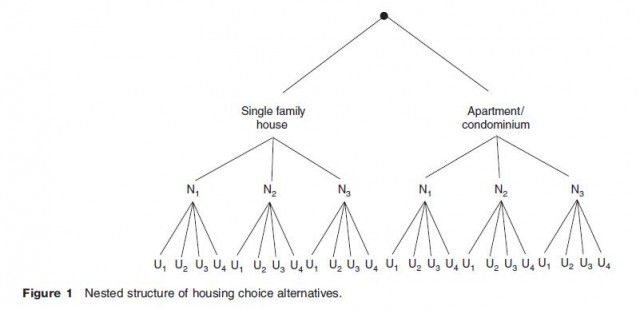
First, the handful of choice models mentioned in the previous section that implicitly or explicitly capture the extent of the decision maker's choice set are not affected by the IIA property. The same can be said of the multinomial probit model; this model encapsulates the degree of substitution between pairs of alternatives through a variance–covariance matrix estimated on empirical choice data. In certain choice situations, patterns of substitution among alternatives can be figured out without great difficulty on the basis of existing cognitive and behavioral theories and built into the choice model. The nested multinomial logit model (NMNL) assumes that alternatives can be sorted hierarchically according to their degree of substitutability. A classical case is that of the housing choice problem. Figure 1 illustrates such a problem, where housing units are clumped into types (single family vs. apartments) in first instance because of the low level of substitutability between housing types. Then, within each type, differentiation based on the neighborhood emerges (N1 through N3), and finally each unit of each type in each neighborhood is evaluated on its own merit (U1 and so on). The NMNL exhibits the IIA property for choice alternatives belonging to the same cluster (or nest). This model is a member of a broader class of choice models that also allow for cross elasticities between alternatives. The primary drawback of the NMNL is that the particular structure of substitutability among alternatives must be defined by the analyst beforehand, while the hierarchical order is sometimes unclear or arbitrary. It should be noted that the hierarchical structure that underpins the NMNL creates a form of conditionality of choice subsets and by the same token solves the problem of the choice set definition.

Relationships among Choices

It is not unusual at all for decisions to be interrelated. An individual's choice of housing location is intertwined with the location of the place of work. These choices in turn are influenced by a number of the individual's nonspatial decisions, such as the decision to marry, raise a family, and adopt a certain lifestyle. Individual decisions may also need to be coordinated within the framework of a household. Finally, other decisions of more limited scope may be affected: decision to buy a car or not, choice of the commute travel mode, choice of a commute route, etc. The multiple facets of travel decisions have also been recognized as an area where an integrated modeling approach is beneficial. Simple origin–destination trips are subsumed by tripchaining and household daily activity patterns, where activity scheduling, stop frequency, timing and location, routing, and modal choices come together. Similarly, choices made by private business or government entities are seldom the results of isolated decisions.

The integration of complex sets of decisions within the framework of random utility theory has followed three main lines of research. In the first and simplest, complex decisions are modeled jointly, in a single step. The decision maker is seen as selecting from a super choice set formed of the Cartesian product of choice sets defined on each elemental choice dimension. For instance, the integration of residential location choice (three neighborhoods to choose from) and of the choice of a commute travel mode (three modes available) creates a choice set made of nine composite housing location/travel mode options. As a variant of this approach, tripchaining behavior can be modeled as a Markov process, with probabilities of transition between states rendered by a joint choice model.

Evidently, the joint modeling approach may not be well suited to the complexity of the multidimensional decisions due to the IIA property. With a decomposition of the choice set into hierarchical groups, a nested choice model captures the complexity through a series of simple choice models conditioning decisions along dimension to choices modeled at earlier stages. Finally, for decision situations where some choices are on a continuous scale (e.g., weekly commute time), mixed continuous/discrete choice models can be estimated.

Other Decision Rules

Random utility choice models make specific assumptions on the internal mechanisms used by decision makers to process information and derive a choice. The customary linear utility function supposes trade offs (or compensatory offsets) among attributes of choice alternatives, on the basis of which a deterministic decision is made that maximizes utility. In this view, poor performance of an alternative on one choice criterion can be compensated by a good performance on one or more other criteria. Various decision rules that do not espouse the principle of full compensation between attributes have been suggested. Some rules may require that an alternative must exceed specific values of each attribute to be chosen (e.g., a house should have a sale price under $300 000 and be no more than 1 mile away from work). Alternatives that fail to reach a certain attribute level are rejected as unacceptable, even if they outperform other alternatives on some other attribute. Some other rule systems are less stringent and consider an alternative as worthwhile if it meets a preset threshold on one attribute only, regardless of its performance on others (a house should have a sale price under $300 000 or be less than 1 mile away from work). Another popular rule system is the elimination by aspect. This rule proceeds in a stepwise fashion, considering each attribute in turn from the attribute deemed the most important to the least important. The selection process eliminates all alternatives that do not satisfy a threshold defined on the selected attribute and continues until a single alternative remains. Interestingly, these alternative decision rules can also serve as methods for defining choice sets.

Attribute trade offs are not the only property that sets apart rule based and random utility models. While the latter are parametric models of choice behavior, the former emphasize the algorithmic methods of information retrieval, representation, processing, and fusion that lead to a unique choice decision. Not surprisingly, diverse constructs of data mining and knowledge discovery have become prominent in implementing noncompensatory choice models, such as decision trees and related methodologies. With decision trees, sequential sets of conditions on attributes are applied so as to identify the choice strategies that lead to alternatives being selected. Complex learning algorithms of rule induction developed in artificial intelligence have dramatically expanded the horizon of possibilities in modeling choices from a process oriented perspective. Some hybrid semicompensatory rule based systems even have the flexibility of blending random utility maximization with decision thresholds. Once calibrated on empirical choice data, rule based systems can be built into computational process models that simulate real world choice behavior over the full range of spatiotemporal scales.

Decision Making and Modeling Choices

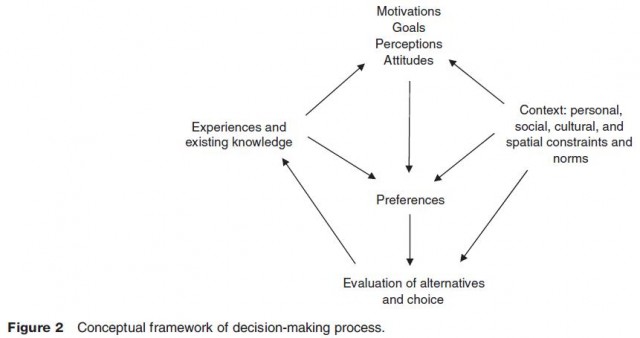
While this may not patently transpire from the discussion held thus far in this article, choices are the results of a decision making process involving multiple sets of considerations. Behavioral geographers and environmental psychologists have worked at crafting the conceptual framework that integrates the actual act of selecting an alternative with the mental and cognitive processes that operate under the influence and constraint of the ambient social and physical environment of the decision maker. Figure 2 schematically represents such structure. Choice models have traditionally addressed the relationship between individual preferences on the one hand, and the evaluation of alternatives and the resulting choice of an alternative on the other, at the exclusion of all other considerations reported in the schematic framework. To this day, the theory of choice modeling still has a limited ability to incorporate these other considerations and, when it does, it is in a rather piecemeal fashion. The state of the art in choice modeling can positively be linked to so called hybrid choice models that integrate multiple models of choice under constraints and models of cognitive and psychological factors in a recursive structure. Owing to their flexibility and structural similarities to the framework depicted in Figure 2, simulators and computationally intensive numerical procedures (e.g., artificial neural networks) can be expected to play a significant role in tomorrow's choice modeling.