How Do We Use Freshwater Resources?

WE USE LARGE QUANTITIES OF WATER each day, for a variety of purposes, especially power generation and irrigation of farms. How much water does each of our activities consume, and where does the water come from?

What Are the Main Ways in Which We Use Fresh Water?

The U.S. Geological Survey (USGS) studied water use in the U.S. Its compilation shows that we use fresh water in six or seven main ways, depending on how we classify the data. For the year 2005, freshwater use in the U.S. was 349 billion gallons per day, most of which is from surface-water sources. Examine the graph below and think about the many ways you use water.

Thermoelectric Power — Electrical-generating power plants are the largest user of fresh water in the U.S., using 41% of the total amount of fresh water. Such power plants drive their turbines by converting water into steam and also use large amounts of water to cool hot components. Some of this water is from recycled sources. Power plants are also the largest users of saline (salty) water.

Irrigation — Farms and ranches are the other large users of fresh water, using nearly 37% of fresh water. Farms use water from groundwater, streams, lakes, and reservoirs to irrigate grain, fruit, vegetables, cotton, animal feed, and other crops. Much of this water is lost through evaporation  to the atmosphere before it can be used by plants. The sprinkler system shown here is designed to cut down on water use, as it delivers water more directly to crops than a central sprinkler.

Public and Domestic Water Uses — The third largest use of fresh water is by public water suppliers and other domestic uses. We consume water by drinking, bathing, watering lawns, filling artificial lakes, and washing clothes, dishes, and cars. Much water from public water suppliers also goes to businesses. Most water for public and domestic use comes from streams and groundwater.

Industrial and Mining Uses — Fresh water and saline water are extensively used by industries, including factories, mills, and refineries. Water is integral to many manufacturing operations, including making paper, steel, plastics, and concrete. Mining and related activities also use water in the extraction of metals and minerals from crushed rock.

Aquaculture — According to the USGS study, we use approximately 2.5% of fresh water to raise fish and aquatic plants. Most of this use is in Idaho, near the Thousand Springs area. Such water is not totally consumed — much is released back into the Snake River.

Livestock — Providing water for cows, sheep, horses, and other livestock accounts for only 0.6% of freshwater use, but much water is used for irrigation to raise hay, alfalfa, and other animal feed. Many ranches use small constructed reservoirs and ponds as the main water source for animals.

How Do We Use and Store Water?

Electrical Generation — The movement of surface water can generate electricity. To do this, we build dams that channel water through turbines in a hydroelectric power plant.

Transportation — We use many large waterways, such as the Mississippi River, as energy-efficient transportation systems to move agricultural  products, chemicals, and other industrial products.

Recreation — People use surface water in lakes and streams for many types of recreation, including swimming, tubing, rafting, boating, and fishing. We also use fresh water to fill ponds, fountains, and swimming pools.

Surface waters are commonly stored in natural lakes and in constructed reservoirs behind concrete and earthen dams. Water for drinking and other municipal uses can be stored in underground or above-ground storage tanks.

We construct canals, raised aqueducts, and large and small pipelines to move fresh water from one place to another, especially to irrigate farms or to bring water to large cities. Pumps in water wells move groundwater to the surface.

How Do We Refer to Volumes of Water?

Water-resource studies typically report volumes of water in one of three units: gallons, liters, or acre-feet. Gallons and liters are familiar terms, but the concept of an acre-foot of water requires some explanation.

How big is an acre? An acre covers an area of 4,047 m2 (43,560 ft2). If a perfect square, an acre would be 64 m (210 ft) on a side. An acre is equivalent to 91 yards of an American football field. There are 640 acres in a square mile.

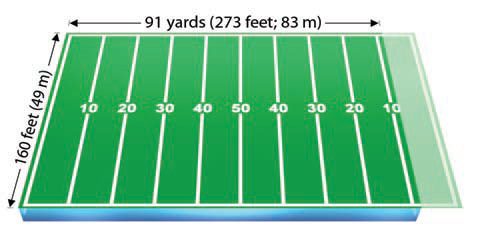
An acre-foot of water is the volume of water required to cover an acre of land to a height of one foot. Imagine covering 91% of a football field (one acre) with a foot of water. An acre-foot is equivalent to about 326,000 gallons or more than 1.2 million liters of water.

Drinking-Water Standards in the U.S.

The U.S. Environmental Protection Agency (EPA) sets standards for safe drinking water. Nearly all public water supplies in the U.S. meet these standards, which can be found at www.epa.gov. These standards set a limit on the concentrations of selected contaminants in water. Small municipalities commonly have more trouble meeting these standards than large cities because of limited budgets for water analysis and for building and running facilities to remove contaminants. The EPA standards do not apply to private wells.

Many people prefer the taste of bottled water to public tap water, but there are generally no health reasons to buy bottled water so long as the public water provider meets all the federal, state, and local drinking water regulations. Commercially bottled water is monitored by the Food and Drug Administration (FDA) but is not monitored as closely as public water systems. The FDA requires a bottler to test its water source only once a year. Also, bottled water can cost as much as 1,000 times more than municipal drinking water.